教材:《机器学习》——周志华 (西瓜书)
傍晚小街路面上沁出微雨后的湿润,和煦的细风吹来,抬头看看天边的晚霞,嗯,明天又是一个好天气.走到水果摊旁,挑了个根蒂蜷缩、敲起来声音浊响的青绿西瓜,一边满心期待着皮薄肉厚瓤甜的爽落感,一边愉快地想着。
绪论
从上述周志华老师的引言来看,为什么微湿路面,和煦细风,天边晚霞的场景认为明天是好天气;根蒂蜷缩,敲声浊响,青绿的西瓜是好瓜。可以十分巧妙的看出,人类通过自身积累的经验对于新情况能够做出有效的预判。
而什么是机器学习,通俗来讲,指的是在计算机系统中,将“经验”以“数据”形式存储,基于这些数据,利用“学习算法”产生模型。在面对新情况时(一个未剖开的西瓜),基于该模型得到相应的判断结果(好瓜/烂瓜)
基本术语
示例或样本:数据集中的每一条数据记录
样例:拥有标记信息的样本
特征或属性:反映事件或对象在某方面的表现或性质的事项
属性值:属性上的取值
属性空间:将属性张成描述事件或对象的d维空间
特征向量:每个示例都能在属性空间找到自己的坐标,因此一个示例又称“特征向量”
学习算法:从数据中产生“模型” 的算法,即“学习算法”
学习或训练:通过执行“学习算法”,从数据中学得模型的过程
P(|ƒ (X) – Y| ≤ ε) ≥ 1- δ 我们希望以很高的概率获得一个很好的模型
假设:学习模型对应了关于某条潜在的规律为假设;
真相:学得模型的某种潜在的规律为真相
学习器:学习算法对一个数据和一个参数在给定实列化之后,得到的一个结果
分类、回归:前者欲预测的是离散型,后者为连续型
聚类:感知样本间的相似度进行类别归纳
监督学习、无监督学习:前者代表有分类和回归,后者代表有代表有聚类(根据训练数据是否拥有标记信息划分这两大类)
二分类、多分类、正类、反类
未知分布:通常假设样本空间的样本服从某假设(规律)的一个分布为未知分布
未见样本:训练模型中的样本为某一假设(规律)分布(未见分布)中的一部分,而同处于这个假设的其他样本为未见样本
独立同分布(i.i.d):如果多个随机变量之间相互独立,并且具有相同的分布函数,那么这些随机变量就是独立同分布的
泛化:模型对新数据的处理能力更好,泛化能力更强 |ƒ(X) – Y| ≤ ε
归纳偏好
机器学习算法在学习过程中对某种类型假设的偏好,任何一个有效的机器学习算法必有其偏好
一般原则(奥卡姆剃刀):若非必要,无增实体
学习算法的归纳偏好是否与问题本身匹配,大多数时候直接决定了算法能否取得好的性能
NFL定理
一个算法£a若在某些问题是比另一个算法£b好,必存在另一个问题£b比£a好
NFL定理的重要前提:所有“问题”出现的机会相同、或所有问题同等重要
具体问题,具体分析!
最优方案往往来自:按需设计,度身定制
模型评估与选择
过拟合和欠拟合
泛化误差:在“未来”样本上的误差
经验误差:在训练集上的误差,亦称训练误差
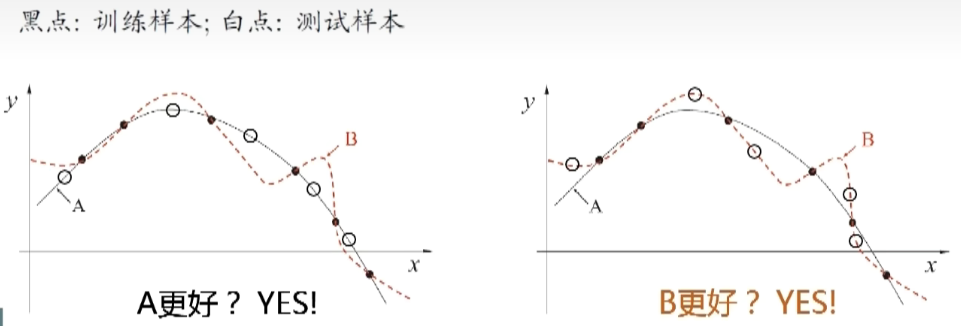
过拟合:过拟合是指模型在训练数据上表现得过于优秀,但在未见数据上表现较差
欠拟合:欠拟合是指模型无法很好地拟合训练数据,无法捕捉到数据中的真实模式和关系
三大问题
模型选择上的三个关键问题:
如何获得测试结果? ——>评估方法
如何评估性能优劣? ——>性能度量
如何判断实质差别? ——>比较检验
评估方法
常见的方法:留出法、交叉验证法、自助法
留出法(hold-out)
直接将数据集划分为两个互斥的集合,一个作为训练集,另一个作为测试集
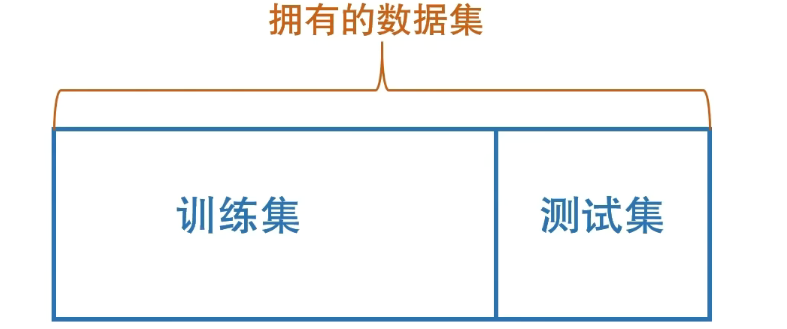
- 保持数据分布一致性(例如:分层采样)
- 多次重复划分(例如:100次随机划分)
- 测试集不能太大、不能太小(例如:1/5~1/2)
k-折交叉验证法(cross vaildation)
将样本集分为k份,其中k-1份作为训练数据集,剩下的1份作为验证数据集
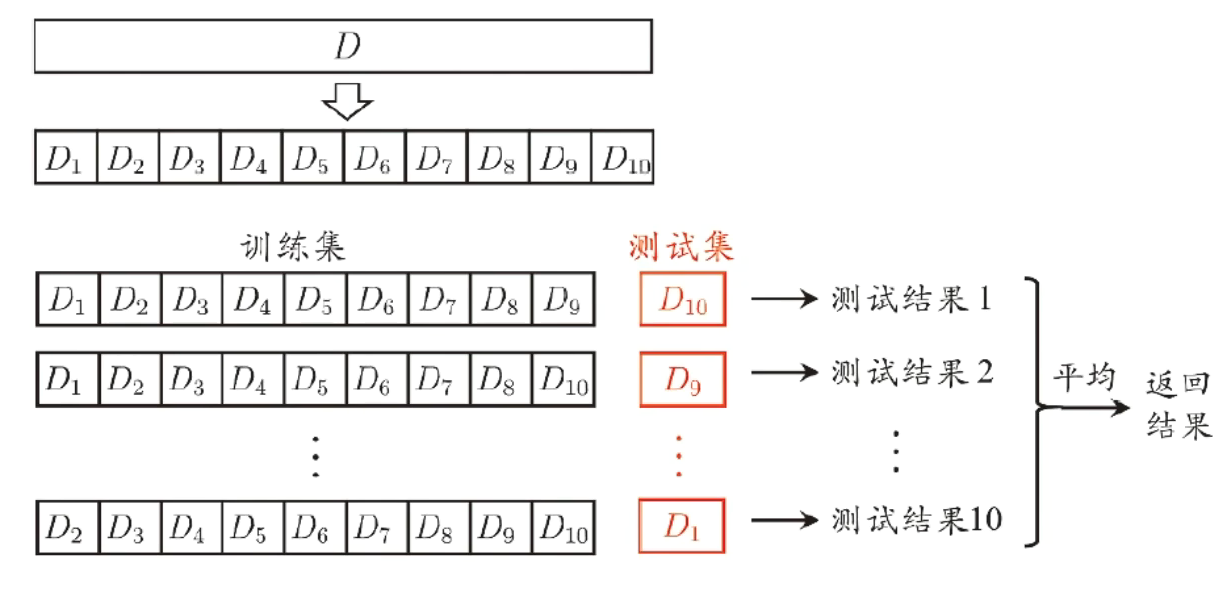
自助法(bootstrap)
自助法亦称有放回采样、可重复采样
是一种从给定训练集中有放回的均匀抽样方法,为划分训练集后,留有充足的测试集进行测试
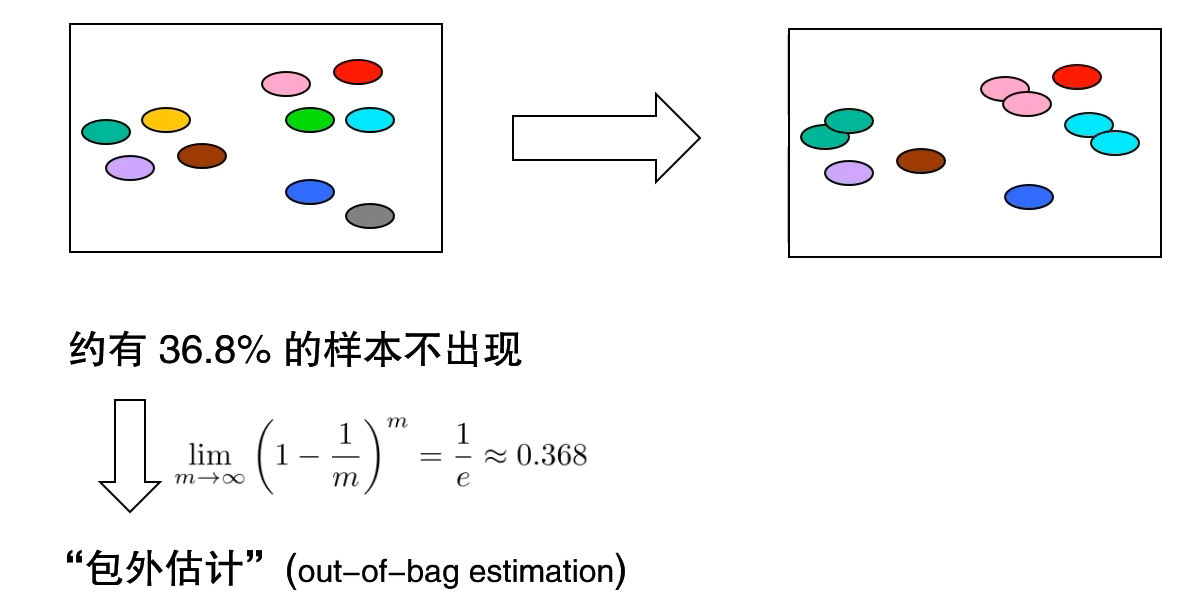
调参与验证集
算法的参数:一般由人工设定,亦称“超参数”
模型的参数:一般由学习确定
调参:调参是指在机器学习过程中,对算法参数进行设定的过程。调参的目的是为了找到最优的参数组合,使得机器学习模型能够更好地适应训练数据,提高模型的准确性和泛化能力。
验证集:是指用于模型选择和调参的数据集。它是从训练集中再分拆出来的,用于对学习算法调整参数、选择特征或做其他决策
性能度量
性能度量是衡量模型泛化能力的评价标准,反映了任务需求
回归任务常用均方误差:
E(ƒ;D) = \frac{1}{m}\sum_{m}^{i=1}(ƒ(x_{i})-y_{i})^{2}分类任务常用错误率和精度:
E(ƒ;D)= \frac{1}{m}\sum_{m}^{i = 1}\mathbb I(ƒ(x_{i})≠y_{i})acc(ƒ;D) = \frac{1}{m}\sum_{m}^{i = 1}\mathbb I(ƒ(x_{i})=y_{i})=1-E(ƒ;D)查准率、查全率:
| 真实情况 | 预测结果 | |
| 正例 | 反例 | |
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假正例) | TN(真反例) |
查准率:P = TP/(TP + FP)
查全率:R = TP/(TP + FN)
F1度量是一种综合考虑查准率和查全率的度量方式,通常用于衡量二元分类模型的性能。
其一般形式可以表示为:
F1 = \frac{2 × P × R}{(P + R)} =\frac{2× TP}{样例总数+TP-TN}
\frac{1}{F1} = \frac{1}{2}× (\frac{1}{P}+\frac{1}{R} ) 若对查准率/查全率有不同偏好:β>1时查全率有更大影响;β<1时查准率有更大影响
F_{\beta } =\frac{(1+\beta^{2}\times P\times R )}{(\beta^{2}\times P)+R}
\frac{1}{F_{\beta } } =\frac{1}{1+\beta^{2}} \times (\frac{1}{P}+\frac{\beta^{2}}{R} )比较检验
常用方法:统计假设检验,为学习器性能比较提供了重要依据
两学习器比较
- 交叉验证t检验(基于成对t检验):比较两组数据的均值是否存在显著差异。例:通过判断两学习器的误差差值的均值或标准差进行检验,
- McNemar检验(基于列联表,卡方检验)用于比较两个分类器在不同数据集上性能差异的统计检验。例:比较两个分类器在不同数据集上的查准率和查全率等指标,判断它们是否存在显著差异
线性模型
线性模型试图学得一个通过属性的线性组合来进行预测的函数
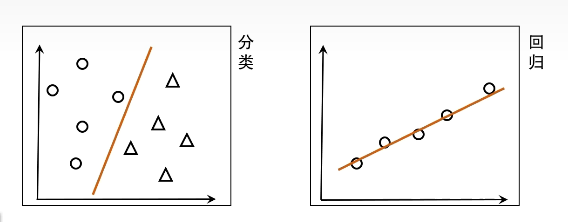
f(x) = \omega _{1} x_{1}+\omega _{2}x_{2}+...+\omega _{d}x_{d}+b向量形式:f(x) = \omega ^{T} x+b线性模型优点:
形式简单、易于建模
可解释性
非线性模型的基础,引入层级结构或高维映射
线性回归
线性回归要做的是 找到f(x_{i} ) = \omega x_{i}+b使得f(x_{i} )\simeq y_{i}线性回归擅长处理数值属性
对于离散属性数值处理时,对于有序关系,如身高:高中低,进行连续化处理1(高),0.5(中),0(低)
对于无序关系,离散属性有k个可能取值,转化为k维向量表示,如西瓜颜色:青绿色[1 0 0], 浅绿色[0 1 0], 白色[0 0 1]
最小二乘法
最小二乘法:是基于均方误差最小化来进行模型求解的方法
令均方误差最小化,有
(w^{*},b^{*}) = \mathop{arg min}\limits_{(w,b)}\sum_{i=1}^{m} (f(x)_{i}-y_{i})^2
=\mathop{arg min}\limits_{(w,b)}\sum_{i=1}^{m} (y_{i}-wx_{i}-b)^2对E(w,b)=∑mi=1(yi-wxi-b)2进行最小二乘参数估计
分别对w和b求导,可得:
\frac{\partial E_{(w,b)}}{\partial w} = 2(w\sum_{i=1}^{m} x_{i}^2-\sum_{i=1}^{m}(y_{i}-b)x_{i}) \frac{\partial E_{(w,b)}}{\partial b} = 2(mb-\sum_{i=1}^{m}(y_{i}-wx_{i})) 令倒数为0,得到闭式解:
w=\frac{\sum_{i=1}^{m}y_{i}(x_{i}-\bar{x} ) }{\sum_{i=1}^{m}x_{i}^2-\frac{1}{m}(\sum_{i=1}^{m}x_{i})^2 } b = \frac{1}{m} \sum_{i=1}^{m} (y_{i}-wx_{i})回归方程评估
SSR为回归平方和,SSE为残差平方和,SST为总离差平方和。
SSR:是拟合数据与原始数据均值之差的平方和。
SST:是原始数据和均值之差的平方和,即SST=SSE+SSR。
R2:是通过数据的变化来表征一个拟合的好坏
R2(判定系数)的正常取值范围为[0,1],越接近1,表明方程变量的解释能力越强,模型对数据的拟合程度也越好
R^2=\frac{SSR}{SST}=\frac{SST-SSE}{SST} =1-\frac{SSE}{SST} 逻辑回归
梯度下降法
视频详细讲解梯度下降法的主要思想和相关内容
梯度下降的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值
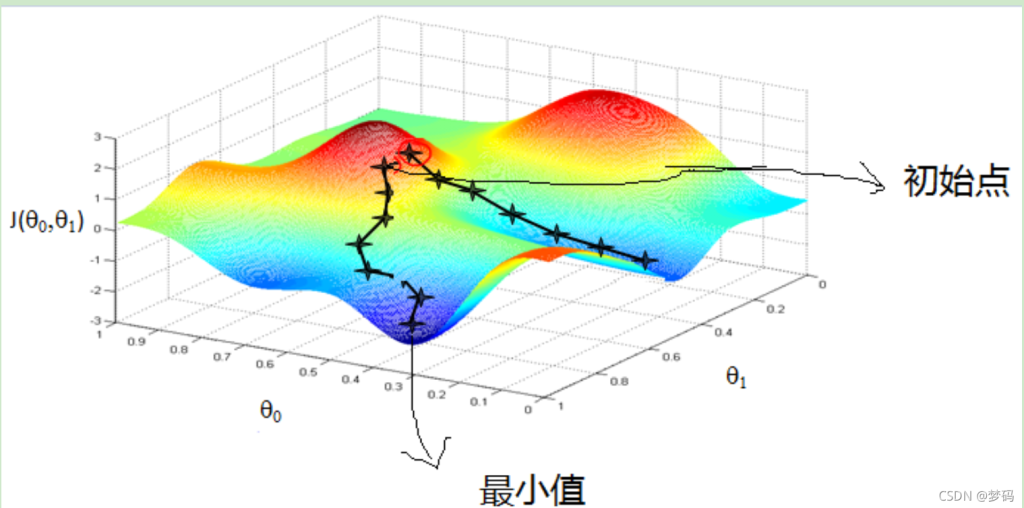
梯度下降的步骤:
- 定义代价函数
- 给定起始点
- 计算梯度
- 按学习率前进
- 重复3、4步,直到找到最低点
梯度下降的分类:批量、随机、小批量梯度下降法
学习率:学习率是机器学习中的超参数,影响目标函数的收敛速度和效果
逻辑回归
逻辑回归虽然被称为回归,实际是分类模型,常用于二分类
原理:找到一条能够将不同类别的样本区分开来的线
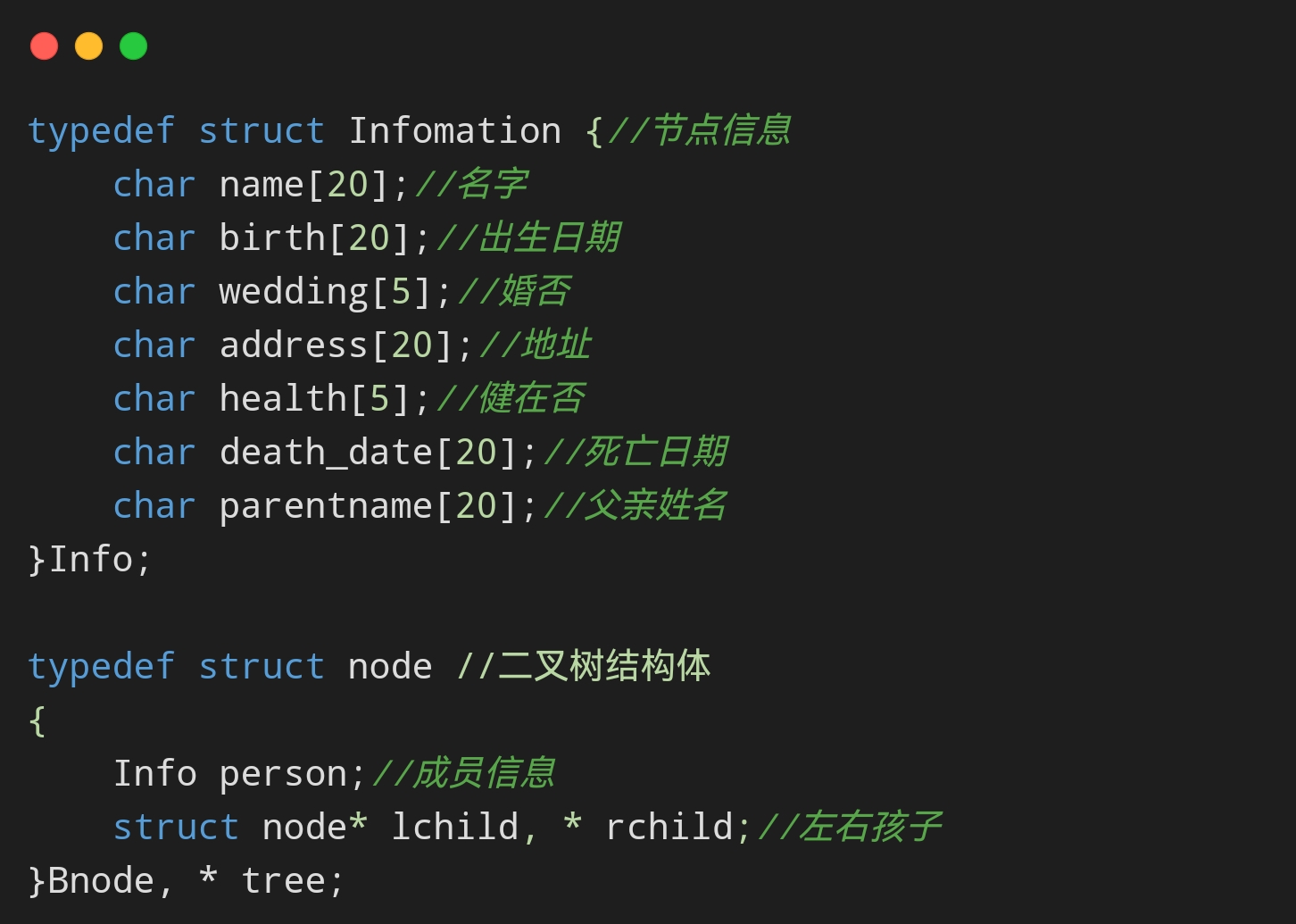
逻辑回归的输出是一个概率值,范围在0到1之间,表示样本属于某个类别的概率。对于二分类问题,通常设置一个阈值(如0.5),将概率值大于阈值的样本归为正类,小于阈值的归为负类(最理想的函数:单位阶跃函数)。