线性结构

线性表

n个元素的有限序列（n≥0）

顺序表

用一组地址连续的存储单元依次存储线性表的数据元素，使得逻辑上相邻的两个元素，物理上也相邻

• 优点：可以随机存取表中的元素，按序号查找元素的速度很快。
• 缺点：插入和删除操作需要移动元素。

链表

节点只在需要时候申请，无需事先分配。节点地址可连续可不连续

节点：数据域 | 指针域

• 优点：插入和删除操作不需要移动元素
• 缺点：只能按顺序访问元素，不能进行随机存取

链表类别

• 单链表 （有头指针指向初始节点）
• 循环链表
• 双链表（有head指针指向初始节点）

栈

特殊的线性表，规则是“后进后出“

顺序栈

用一组地址连续的存储单元依次存储，自栈顶到栈底的数据元素

存储空间是预先定义或申请的，因此可能会出现栈满的情况

• 每一个元素入栈时都要判断栈是否已满。
• 需要设置一个头指针指到栈顶。
• 需要附设指针top指示栈顶元素的位置。（top = -1表示空栈）

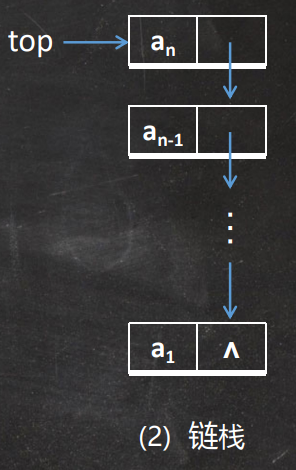
链栈

用链表存储栈中的元素

栈中元素的插入和删除仅在栈顶进行，因此不必设置头节点，链表的头指针就是栈顶指针

队列

• 队列是一种“先进先出”的线性表，队尾入 队头出。

顺序队列

循环队列

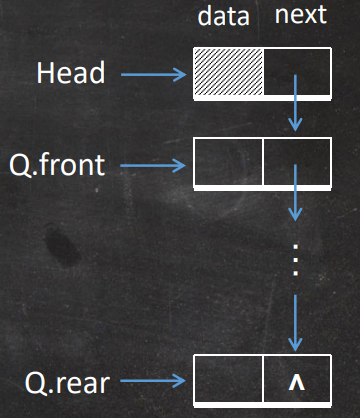
链队列

给链队列添加一个头节点并令头指针指向头节点

队列为空的判定条件就是头指针和尾指针的的值相同，并且均指向头节点。

串

仅由字符构成的有限序列，取值范围受限的线性表

• 串长：即串的长度，指字符串中的字符个数。
• 空串：长度为0的空串，空串不包含任何字符。
• 空格串：由一个或多个空格组成的串。
• 子串：由串中任意长度的连续字符构成的序列称为子串。
• 串相等：指两个串长度相等且对应位置上的字符也相同。
• 串比较：两个串比较大小时以字符的ASCII码值作为依据。

顺序串

用一组地址连续的存储单元来存储串值的字符序列

链式串

字符串可以采用链表作为存储结构，当用链表存储串中的字符时，每个结点中可以存储一个字符或多个字符。

数组和矩阵

数组

• 一维数组是长度固定的线性表，数组中的每个数据元素类型相同。n维数组是定长线性表在维数上的扩张，即线性表中的元素又是一个线性表
• 由于数组一般不做插入和删除，且元素个数和元素之间的关系不再发生变动，那么数组适合采用顺序存储结构

数组元素的存储方式及相关计算

二维数组的存储结构可分为以行为主序（按行存储）和以列为主序（按列存储）两种方法。

设每个数据元素占用L个单元，m、n为数组的行数和列数

• 按行存储地址计算

Loc(a_{ij}) = Loc(a_{11})+((i-1)×n+(j-1))×L

• 按列存储地址计算

Loc(a_{ij}) = Loc(a_{11})+((j-1)×m+(i-1))×L

\begin{matrix}
  a_{11}  a_{12}  a_{13} \\
  a_{21}  a_{22}  a_{23} \\
  a_{31}  a_{32}  a_{33} \\
  a_{41}  a_{42}  a_{43}
\end{matrix}

矩阵

对称矩阵

矩阵A_n*n的元素 a_ij = a_ji(1≤i,j≤n)的特点，则称之为对称矩阵

\begin{matrix}
1 ,3,5,7 \\
3, 4, 9, 8\\
5, 9, 7, 6\\
7, 8, 6, 0 
\end{matrix}

矩阵A_n*n的元素可以压缩存储在n(n+1)/2的空间中，按行存储下三角

k = \left\{\begin{matrix}
  \frac{i(i+1)}{2}+j-1  当 i\ge j \\
  \frac{j(j+1)}{2}+i-1  当 i< j
\end{matrix}\right.

三对角矩阵

对角矩阵是指矩阵中的非零元素都集中在以主对角线为中心的带状区域中，其余的矩阵元素都为零。

即只有主对角线及其左右两边为非零元素。

\begin{pmatrix}
a_{1,1} & a_{1,2} & & & & & & \\
a_{2,1} & a_{2,2} & a_{2,3} & & & & & \\
 & a_{3,2} & a_{3,3} & a_{3,4} & & & & \\
 & & \cdots & \cdots & \cdots & & & \\
 & & & a_{1,i-1} & a_{1,i} & a_{1,i+1} & & \\
 & & & & \cdots & \cdots & \cdots & \cdots \\
 & & & & & & a_{n,n-1} & a_{n,n}
\end{pmatrix}

按行存储N阶三对角矩阵A_n*n的非零元素，在一维数组B[k]（0≤k<3n-2）中，

k = 3(i-1)-1 + j-i+1 = 2i+j-3   (1≤i,j≤n)

稀疏矩阵

• 在一个矩阵中，若非零元素的个数远远少于零元素的个数，且非零元素的分布没有规律，称之为稀疏矩阵
• 用一个三元组(i,j,a_ij）唯一确定矩阵中的一个元素

树和二叉树

树

• 树是n(n≥0)个结点的有限集合。当n=0时称为空树；
• 在任一非空树中，有且仅有一个称为根的结点，
• 其余结点可分为m(m≥0)个互不相交的有限集T，
• 每个集合又都是一棵树，并且称为根结点的子树。

相关概念

• 结点的度：一个结点的子树的个数记为该结点的度。
• 叶子结点：也称为终端结点，指度为零的结点。
• 结点的层次：根为第一层，根的孩子在第二层，依此类推。
• 树的高度：一棵树的最大层次数记为树的高度（或深度）。
• 有序（无序）树：若将树中结点的各子树看成是从左到右具有次序的，即不能交换，则称该树为有序树，否则称为无序树。
• 森林：m(m≥0)棵互不相交的树的集合。

二叉树

• 由一个根结点及两棵不相交的、分别称为左子树和右子树的二叉树所组成
• 或者是空树(n=0)

树和二叉树的区别：

（1）二叉树中结点的子树要区分左子树和右子树，即使只有一棵子树，而树中不用区分。

（2）二叉树中结点的最大度为2，而树中无限制。

二叉树的性质

• 第i层至多有2^(i-1)个节点
• 深度为K的二叉树至多有（2^k）-1个节点
• 对任何一棵二叉树，若其终端结点数为n₀，度为2的结点数为n₂，则n₀=n₂+1。 

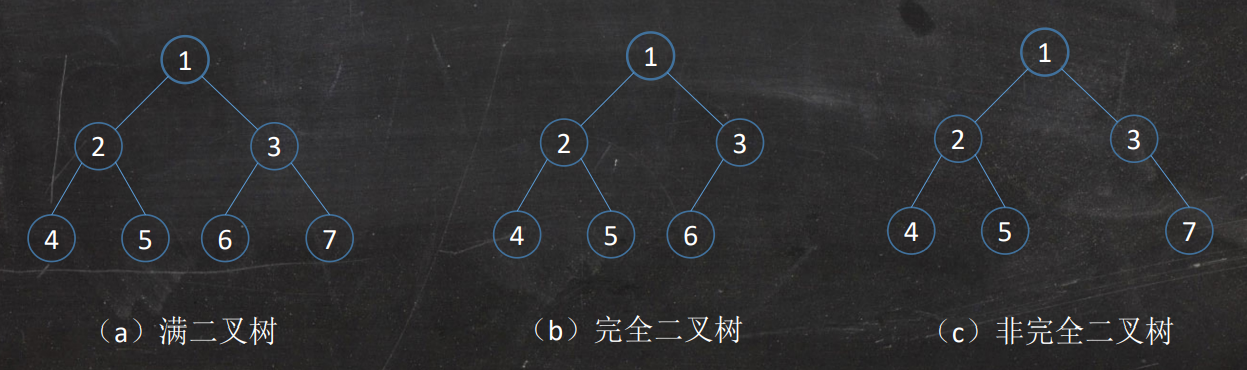
满二叉树和完全二叉树

满二叉树：顾名思义

完全二叉树：当深度为k、有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号为1～n的结点一一对应时，称之为完全二叉树。

二叉树存储结构

顺序存储

在顺序存储中，需要要为空值留下位置

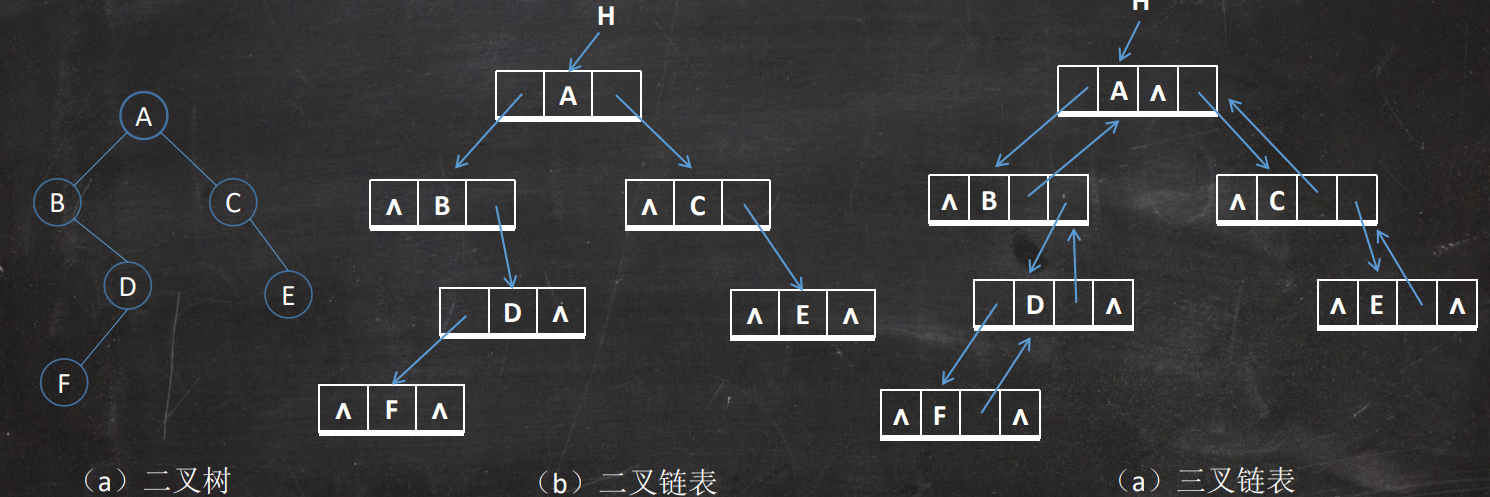
链式存储

二叉节点：左指针域 | 节点内容 | 右指针域

三叉节点：左指针域 | 节点内容 | 右指针域 | 父节点域

二叉树遍历法

• 中序遍历法：左、根、右
• 前序遍历法：根、左、右
• 后序遍历法：左、右、根
• 层序遍历法：按行从左往右、按层从上往下

最优二叉树/哈夫曼树

• 是一类带权路径长度最短的树。
• 权：是一个人为的概念，表示计算机对每个结点的访问频率。
• 路径长度：是每一个结点到根结点的路径的长度。
• 结点的带权路径长度：是指从该结点到根结点之间的路径长度与该结点权的乘积。
• 树的带权路径长度为树中所有叶子结点的带权路径长度之和。
• 生成的在最优二叉树并不唯一

应用：最优二叉树的一个应用是对字符集中的字符进行编码和译码。

如何生成最优二叉树

例如：给定的n个权值{[4，5，8，9，11，13]，构成n棵二叉树的集合F

通过取二个最小的数值，进行比较；

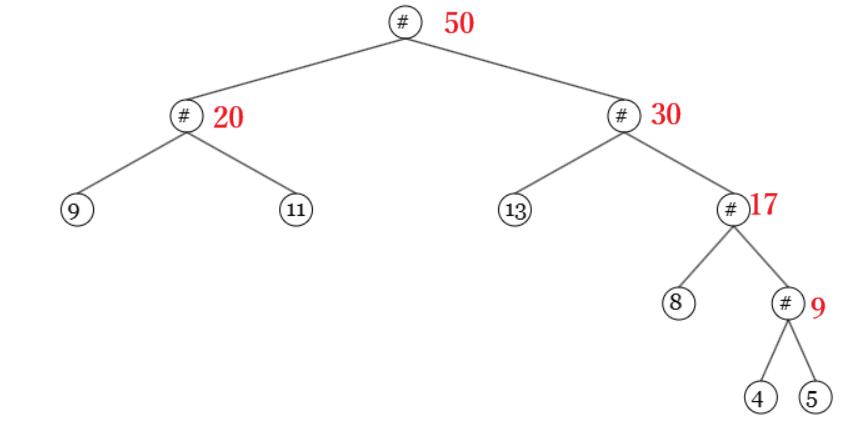
二叉查找树/二叉排序树

• 二叉查找树又称为二叉排序树。
• 它或者是一棵空树
• 左边节点小于父节点，左子树所有节点小于根节点
• 右边节点大于父节点，右子树所有节点大于根节点

对二叉查找树进行中序遍历，可得到一个关键码递增有序的结点序列

二叉查找树的作用：使用二叉查找树来查找树中的数值比普通的二叉树更为方便。

图

定义

• 图Graph记作G=(V，E)
• 顶点集Vertex和边集Edge分别记为V（G）和E（G）

有向图

• 图中每条边都是有方向的。有向边也称为弧。
• 起点称为弧尾，终点称为弧头。
• 顶点v_j 到顶点v_i 表示为<v_j ,v_i>

无向图

• 图中每条边都是无方向的。
• 顶点v_j 到顶点v_i与顶点v_i到顶点v_j边代表一个边

完全图

无向完全图

• 一个无向图具有n个顶点，而每一个顶点与其他n-1个顶点之间都有边
• 共有n(n-1)/2条边

有向完全图

• n(n-1)

（强）连通图、网

度顶点有几条边相连

出度、入度：

子图：子图G‘的V’、E’∈图G的V、E

路径：顶点可到达另一个顶点

连通图：各顶点通过路径（任意两个顶点）相连，对于无向图

强连通图：各顶点通过路径（任意两个顶点）相连，对于有向图

网：每一条边都有权值

图的存储结构

邻接矩阵表示法

• 0：无边；1：有边

网（带有权值的图）的邻接矩阵的表示

• 有边：权值
• 无边：∞

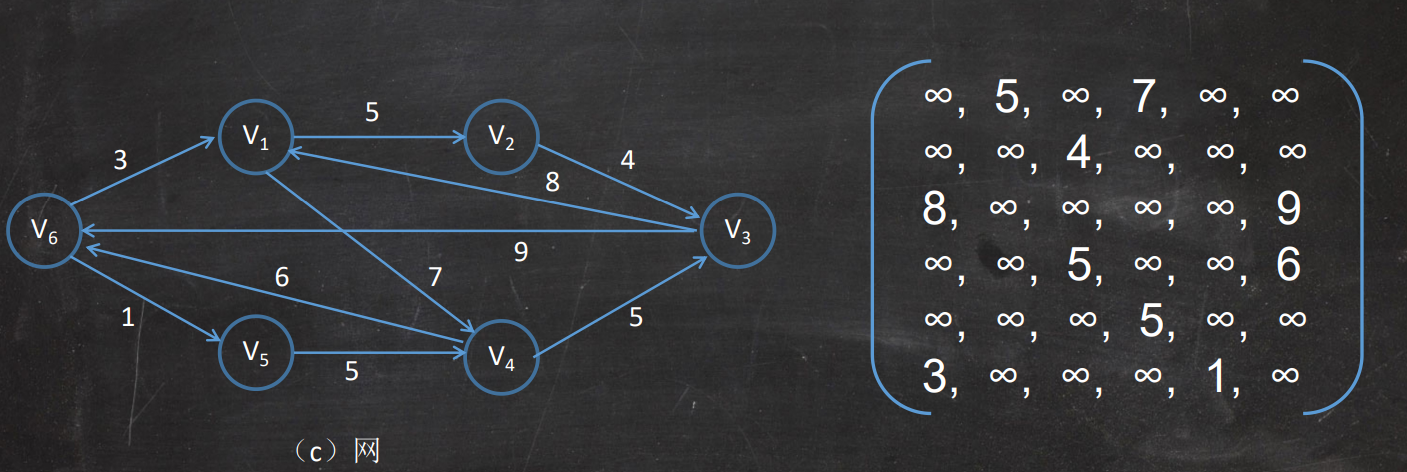
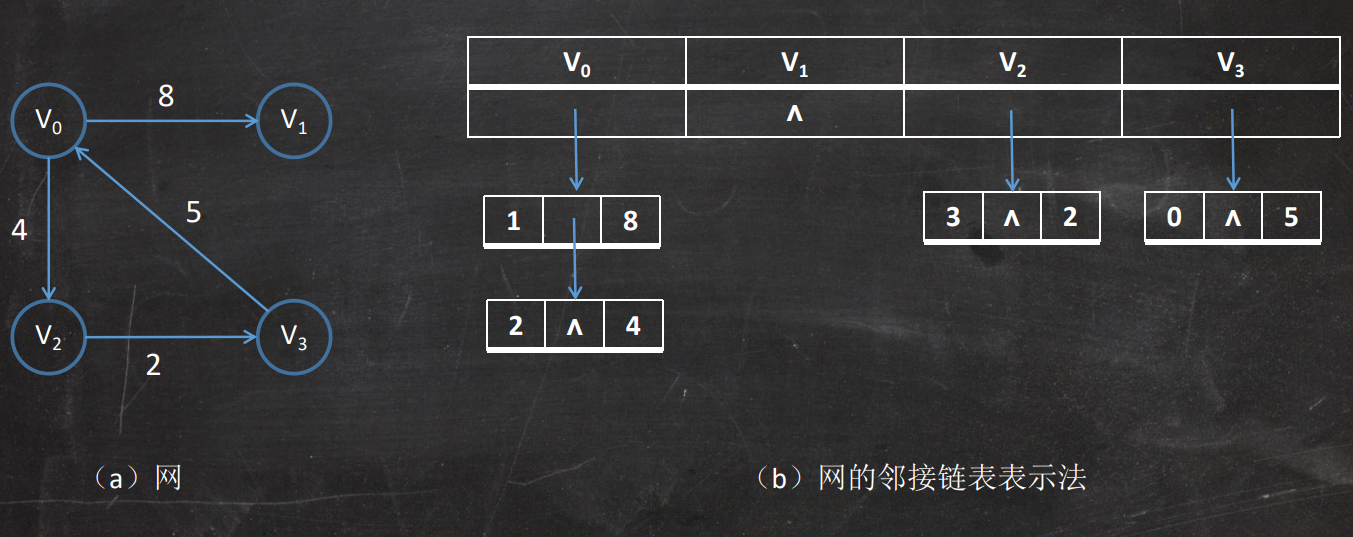
邻接链表表示法

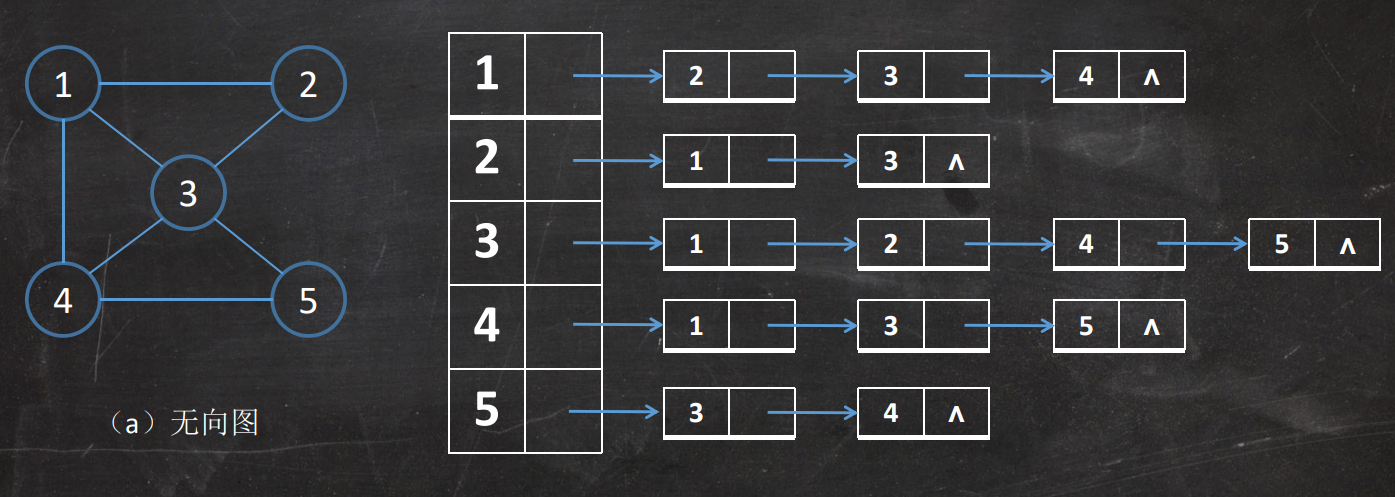
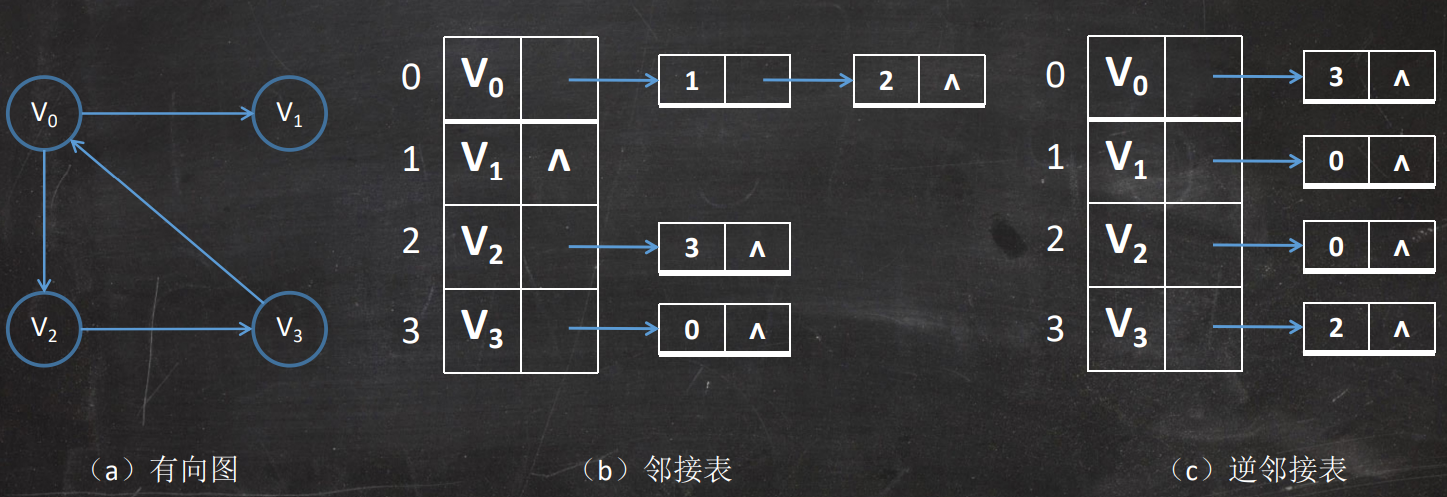
带权值的网的邻接链表表示法